Think you’re a good Diplomacy adjudicator? Here’s a challenge for you:
(If this looks like a headache, go ahead and skip ahead, the rest of the
essay will gradually build up to it.)
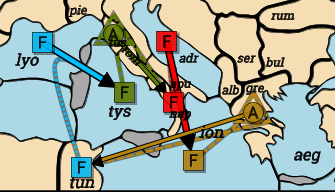
Russia: A Fin-Den. F Stp(sc) S F Bot.
F Bot C A Fin-Den. F Bal C A Fin-Den.
Germany: A Nwy-Bel. F Den S F Nth. F Nth C A Nwy-Bel.
England: A Lon-Bre. F Bel S F Eng. F Eng C A Lon-Bre.
Italy: A Naf-Stp. F Bre S F Mao. F Mao C A Naf-Stp.
F Nao C A Naf-Stp. F Nwg C A Naf-Stp. F Bar C A Naf-Stp.
Austria: F Lvn-Bot. F Swe S F Lvn-Bot. F Edi-Nth. F Yor S F Edi-Nth.
F Iri-Eng. F Wal S F Iri-Eng. F Por-Mao. F Spa(nc) S F Por-Mao.
This is prompted by something that happened in my most recent Diplomacy game:
Italy: F Tun-Ion. F Nap S F Tun-Ion.
Turkey: A Gre-Nap. F Ion C A Gre-Nap.
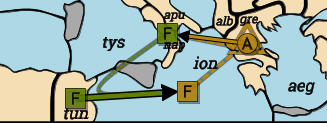
The attack Tun−Ion has support from Nap, so should displace the fleet in Ion, preventing the convoy. Unless it’s deemed that the Gre−Nap attack cuts Nap’s support anyway, is which case the Tun−Ion attack isn’t strong enough to disrupt the convoy. So there are two consistent but incompatible resolutions:
This was interesting because I thought (a) convoy paradoxes only arose in contrived situations, but this one seemed pretty natural (and probably could be made even “more natural” than it actually was by putting the other Italian fleet in Tys instead of Tun), and (b) that they had two inconsistent resolutions, not two consistent ones!
Curiously, both sides can draw support from the rule stating that a unit’s support isn’t cut when it’s attacked by the target of the attack it’s supporting. The “convoy is cut” side says the Turkish fleet is essential to the attack, so it should be treated the same way it would be if Turkey played Ion−Nap. The “support is cut” side says that convoying is morally equivalent to supporting (or at least closer to it than “attacking” is), so the attack on Ion should be treated as an attack on a supporter, not an attacker.
Anyway, busting out the actual rulebook we found that it had this exact scenario (just with the units in different places) as an example for a special anti-support-cutting rule under “rare cases and tricky situations” (which it is — I’ve been aware of convoy paradoxes as theoretical possibilities from early on, but this was the first time I’ve encountered one in a game):
A convoyed Army does not cut the support of a unit supporting an attack against one of the Fleets necessary for the Army to convoy.So, the ruling is the support is not cut, the convoy is disrupted, and Tunisia successfully occupies the Ionian Sea.
This got me thinking — that rule only applies to attacks on “one of the Fleets necessary for the Army to convoy”. Why not another army? Can’t I re-introduce the paradox if I have a convoy attack a unit supporting an attack against a fleet performing a second convoy that would cut the support of a unit supporting an attack against the fleet performing the first convoy? Yes, it turns out you can pretty much just place units and orders to fit that description as you read it:
| have a convoy | Turkish A Gre-Tun C by F Ion | ||
| attack a unit supporting an attack | French F Tun S F Lyo-Tys | ||
| against a fleet performing a second convoy | Italian A Tus-Nap C by F Tys | ||
|
that would cut the support of a unit supporting an attack against the first convoy | Austrian F Nap S F Adr-Ion |

The rulebook as written doesn’t address this situation, but ISTM that the most natural extension is to generalize the anti-support-cutting rule to say that convoyed armies don’t cut support that would disrupt their convoy, whether directly or indirectly. Under that rule, the support stands, the convoys fail, and Lyo−Tys & Adr−Ion both succeed.
Another part of the rule also caught my attention: “A convoyed Army does not cut the support of a unit supporting an attack ...” — well, it’s easy to make a paradox where the possibly-cut support is supplying defense that’s necessary to the convoy:
Turkey: A Gre-Tun C by F Ion. Italy: F Tun S F Ion. Austria: F Alb-Ion S by F Adr.
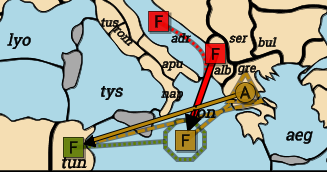
So, one is tempted to amend the rulebook to say “A convoyed Army does not cut the support of a unit supporting an attack on or defense of a Fleet convoying that Army.” Alternately, one can argue that the rules shouldn’t protect players from “own goals”, so defense should be cut.
Rather than take a stand, I was more interested in seeing how it might be applied to two intertwined convoys. Easy enough:
Turkey: A Gre-Tun C by F Ion. F Nap S F Ion. Italy: A Tus-Nap C by F Tys. F Tun S F Tys. Austria: F Alb-Ion S by F Adr. France: F Wes-Tys S by F Lyo.
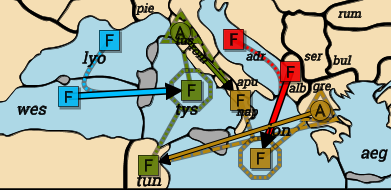
Though simple to construct, it’s very interesting due to it having two consistent & incompatible resolutions in a way that’s quite different than the paradoxes involving supporting attackers. If the Tyrrhenian convoy succeeds, then the support from Naples is cut and the Ionian convoy fails, letting the convoy across the Tyrrhenian happen — OK! But if the Ionian convoy succeeds, then the support from Tunisia is cut and the Tyrrhenian convoy fails, letting the convoy across the Ionian Sea happen — OK too! I personally find this more interesting than all the “all stand or all fall” loops when it’s supporters-of-attackers that are attacked instead of defenders.
You know what would be even more interesting? Three convoys, each of
which disrupts the next one if it isn’t disrupted itself, of course.
Then any {dislodge, remain}3 ruling would be inconsistent with the rules,
three logical NOT gates wired into a triangle — but we can’t send a
disruption across the Italian peninsula, and things are really tight in
the triangle around Sardinia. The obvious choice is to circumnavigate
Great Britain.
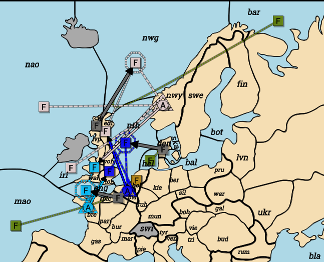
Russia: F Edi S F Nwg. A Nwy-Wal. F Nwg C A Nwy-Wal.
F Nao C A Nwy-Wal. F Iri C A Nwy-Wal.
England: F Lon S F Nth. A Bel-Edi. F Nth C A Bel-Edi.
France: F Wal S F Eng. A Bre-Lon. F Eng C A Bre-Lon.
Germany: F Pic-Eng. F Den-Nth. F Cly-Nwg.
Italy: F Mao S F Pic-Eng. F Hel S F Den-Nth. F Bar S F Cly-Nwg.
I’m going for full symmetry here. Each of England, France, & Russia are convoying an army from the Continent to Britain, where they’ll attempt to cut the support of another power’s fleet that’s supporting that power’s convoying fleet. Each of those fleets is attacked by one German fleet with support from one Italian one. So, each convoy will stand if its support from their fleet in Britain stands, and have its convoying fleet be dislodged otherwise. The only asymmetry is that Russia’s convoy is three fleets long while England’s and France’s use only one fleet each, but that shouldn’t make any difference.
If we add F Hol S F Den-Nth, then there’s no paradox anymore:
Den overwhelms Nth even with Lon’s support, so the Bel−Edi convoy
fails, leaving Edi S Nwg intact, so the convoy from Nwy cuts the
support from Wal, and Eng falls to Pic.
I think the symmetry makes this construction very pretty, but with Russia’s two extra fleets, it feels like there should be room for another convoy. There are several ways to rejigger the units to make room that’s almost enough, but I just can’t quite fit a fourth one around Britain. Though if I’m just trying to cram convoys into paradoxical cycles without regard for what kind of paradox it is, I can go back to the “support the attacker” paradoxes which use only four units per convoy (convoyed army, convoying fleet, attacker, attacker-supporter) while the “defend the convoy” paradoxes need five (those four plus a convoying-fleet-supporter). Then I can fit four convoys around Great Britain without too much trouble.
Austria: A Edi-Nwy. F Nwg C A Edi-Nwy. France: F Ska-Nth. F Nwy S F Ska-Nth. A Wal-Bre. F Eng C A Wal-Bre. Russia: A Hol-Lon. F Nth C A Hol-Lon. England: F Pic-Eng. F Lon S F Pic-Eng. Germany: F Gas-Mao. F Bre S F Gas-Mao. Turkey: A Spa-Cly. F Mao C A Spa-Cly. F Nao C A Spa-Cly. Italy: F Bar-Nwg. F Cly S F Bar-Nwg.
It feels like there’s still room for another convoy if we loop up to the
Arctic Ocean, through St. Petersburg, and back through the Baltics. It
turns out there’s room for a convoy both in Bot and in Bal, which means I
should be able to put a whopping six convoys into the map in a single
paradoxical disrupt/remain cycle using 26 units!
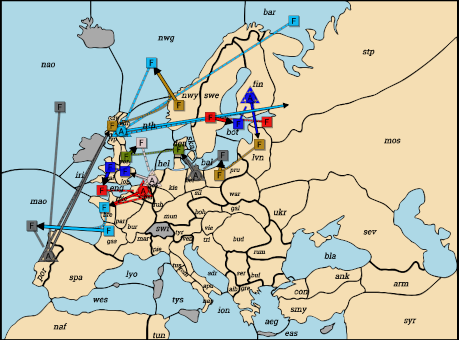
England: A Fin-Lvn. F Bot C A Fin-Lvn. F Wal-Eng. F Lon S F Wal-Eng.
Austria: A Bel-Bre. F Eng C A Bel-Bre. F Swe-Bot. F Stp(sc) S F Swe-Bot.
Turkey: F Pru-Bal. F Lvn S F Pru-Bal. F Nwy-Nwg. F Cly S F Nwy-Nwg.
Germany: A Por-Cly. F Mao C A Por-Cly. F Nao C A Por-Cly.
A Ber-Den. F Bal C A Ber-Den.
Italy: F Yor-Nth. F Den S F Yor-Nth.
Russia: A Hol-Lon. F Nth C A Hol-Lon.
France: A Edi-Stp. F Nwg C A Edi-Stp. F Bar C A Edi-Stp.
F Gas-Mao. F Bre S F Gas-Mao.
Enh. It looks pretty, I guess, but it felt surprisingly straightforward and repetitive, and so was unsatisfying.

What about the more interesting “defend the convoy” paradoxes? Turns out Bothnia Gulf has just enough room for a fourth convoy, and that produces the “adjudication challenge” in the intro: 24 units forming four “logical NOT gates” wired in a square. (There’s no slack up there: all seven units on and around Bot & Bal have to be exactly where they are and doing exactly what they’re doing, except that the attacker & attacker-supporter could swap jobs.) I like that you could pick either Nth & Mao or Bot & Eng as the two convoys to go through (and the other two to fail) and probably convince an adjudicator that’s the right result if they were misled by Italy’s superconvoy into missing the symmetry. Though this construction is not as pretty as the triangle around Great Britain, something makes it my favorite — maybe just because it feels cleverer?
That’s enough of this madness for me. Have a lot of fun!